Bivariate analysis of continuous and/or categorical variables
2024-05-07
Source:vignettes/v02_bivariate.Rmd
v02_bivariate.RmdTidycomm includes five functions for bivariate explorative data analysis:
-
crosstab()for both categorical independent and dependent variables -
t_test()for dichotomous categorical independent and continuous dependent variables -
unianova()for polytomous categorical independent and continuous dependent variables -
correlate()for both continuous independent and dependent variables -
regress()for both continuous or factorial (translated into dummy dichotomous versions) independent and continuous dependent variables
We will again use sample data from the Worlds of Journalism 2012-16 study for demonstration purposes:
WoJ
#> # A tibble: 1,200 × 15
#> country reach employment temp_contract autonomy_selection autonomy_emphasis
#> <fct> <fct> <chr> <fct> <dbl> <dbl>
#> 1 Germany Nati… Full-time Permanent 5 4
#> 2 Germany Nati… Full-time Permanent 3 4
#> 3 Switzerl… Regi… Full-time Permanent 4 4
#> 4 Switzerl… Local Part-time Permanent 4 5
#> 5 Austria Nati… Part-time Permanent 4 4
#> 6 Switzerl… Local Freelancer NA 4 4
#> 7 Germany Local Full-time Permanent 4 4
#> 8 Denmark Nati… Full-time Permanent 3 3
#> 9 Switzerl… Local Full-time Permanent 5 5
#> 10 Denmark Nati… Full-time Permanent 2 4
#> # ℹ 1,190 more rows
#> # ℹ 9 more variables: ethics_1 <dbl>, ethics_2 <dbl>, ethics_3 <dbl>,
#> # ethics_4 <dbl>, work_experience <dbl>, trust_parliament <dbl>,
#> # trust_government <dbl>, trust_parties <dbl>, trust_politicians <dbl>Compute contingency tables and Chi-square tests
crosstab() outputs a contingency table for one
independent (column) variable and one or more dependent (row)
variables:
WoJ %>%
crosstab(reach, employment)
#> # A tibble: 3 × 5
#> employment Local Regional National Transnational
#> * <chr> <dbl> <dbl> <dbl> <dbl>
#> 1 Freelancer 23 36 104 9
#> 2 Full-time 111 287 438 66
#> 3 Part-time 15 32 75 4Additional options include add_total (adds a row-wise
Total column if set to TRUE) and
percentages (outputs column-wise percentages instead of
absolute values if set to TRUE):
WoJ %>%
crosstab(reach, employment, add_total = TRUE, percentages = TRUE)
#> # A tibble: 3 × 6
#> employment Local Regional National Transnational Total
#> * <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 Freelancer 0.154 0.101 0.169 0.114 0.143
#> 2 Full-time 0.745 0.808 0.710 0.835 0.752
#> 3 Part-time 0.101 0.0901 0.122 0.0506 0.105Setting chi_square = TRUE computes a \(\chi^2\) test including Cramer’s \(V\) and outputs the results in a console
message:
WoJ %>%
crosstab(reach, employment, chi_square = TRUE)
#> # A tibble: 3 × 5
#> employment Local Regional National Transnational
#> * <chr> <dbl> <dbl> <dbl> <dbl>
#> 1 Freelancer 23 36 104 9
#> 2 Full-time 111 287 438 66
#> 3 Part-time 15 32 75 4
#> # Chi-square = 16.005, df = 6, p = 0.014, V = 0.082Finally, passing multiple row variables will treat all unique value combinations as a single variable for percentage and Chi-square computations:
WoJ %>%
crosstab(reach, employment, country, percentages = TRUE)
#> # A tibble: 15 × 6
#> employment country Local Regional National Transnational
#> * <chr> <fct> <dbl> <dbl> <dbl> <dbl>
#> 1 Freelancer Austria 0.0134 0.0113 0.0162 0
#> 2 Freelancer Denmark 0.0537 0.0197 0.112 0.0127
#> 3 Freelancer Germany 0.0470 0.0507 0.00648 0
#> 4 Freelancer Switzerland 0.0403 0.00845 0.00162 0
#> 5 Freelancer UK 0 0.0113 0.0324 0.101
#> 6 Full-time Austria 0.0403 0.180 0.152 0.0127
#> 7 Full-time Denmark 0.168 0.192 0.295 0
#> 8 Full-time Germany 0.268 0.172 0.0616 0
#> 9 Full-time Switzerland 0.168 0.197 0.0875 0.0633
#> 10 Full-time UK 0.101 0.0676 0.113 0.759
#> 11 Part-time Austria 0 0.0225 0.0292 0
#> 12 Part-time Denmark 0.00671 0.0113 0.0178 0
#> 13 Part-time Germany 0 0.00282 0.00648 0
#> 14 Part-time Switzerland 0.0872 0.0479 0.0632 0
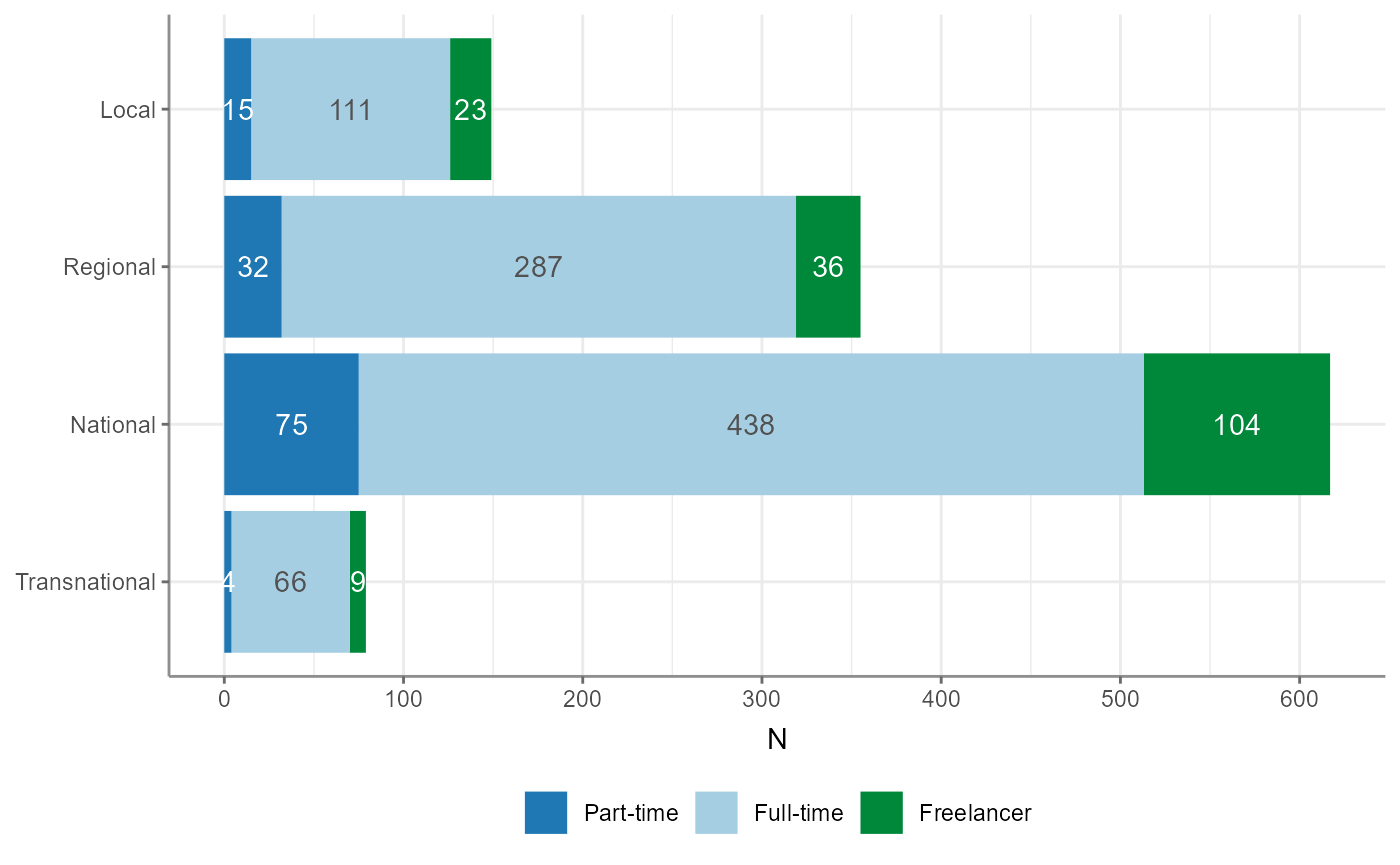
#> 15 Part-time UK 0.00671 0.00563 0.00486 0.0506You can also visualize the output from crosstab():
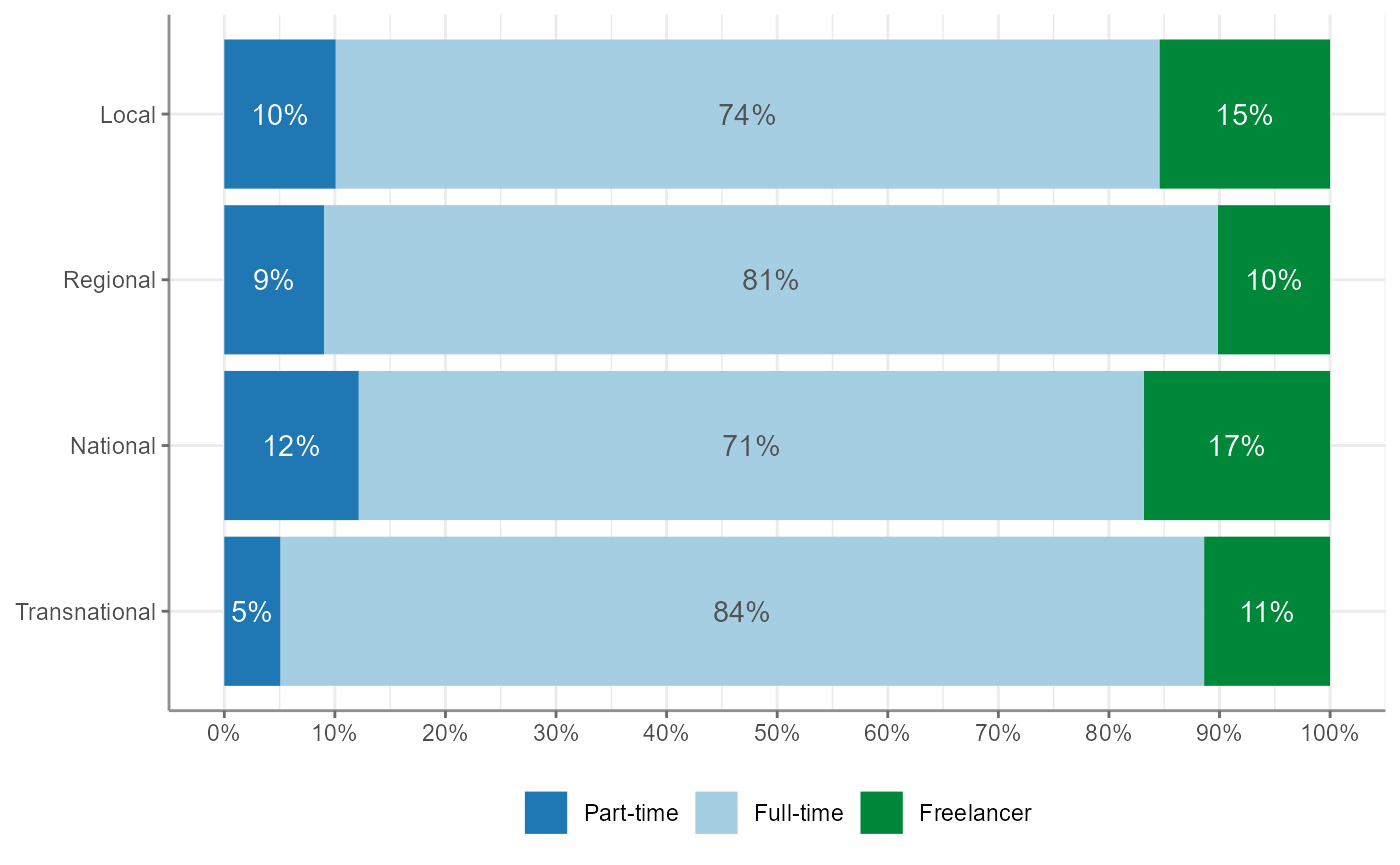
Note that the percentages = TRUE argument determines
whether the bars add up to 100% and thus cover the whole width or
whether they do not:
Compute t-Tests
Use t_test() to quickly compute t-Tests for a group
variable and one or more test variables. Output includes test
statistics, descriptive statistics and Cohen’s \(d\) effect size estimates:
WoJ %>%
t_test(temp_contract, autonomy_selection, autonomy_emphasis)
#> # A tibble: 2 × 12
#> Variable M_Permanent SD_Permanent M_Temporary SD_Temporary Delta_M t df
#> * <chr> <num:.3!> <num:.3!> <num:.3!> <num:.3!> <num:.> <num> <dbl>
#> 1 autonom… 3.910 0.755 3.698 0.932 0.212 1.627 56
#> 2 autonom… 4.124 0.768 3.887 0.870 0.237 2.171 995
#> # ℹ 4 more variables: p <num:.3!>, d <num:.3!>, Levene_p <dbl>, var_equal <chr>Passing no test variables will compute t-Tests for all numerical variables in the data:
WoJ %>%
t_test(temp_contract)
#> # A tibble: 11 × 12
#> Variable M_Permanent SD_Permanent M_Temporary SD_Temporary Delta_M t
#> * <chr> <num:.3!> <num:.3!> <num:.3!> <num:.3!> <num:.> <num:>
#> 1 autonomy_se… 3.910 0.755 3.698 0.932 0.212 1.627
#> 2 autonomy_em… 4.124 0.768 3.887 0.870 0.237 2.171
#> 3 ethics_1 1.568 0.850 1.981 0.990 -0.414 -3.415
#> 4 ethics_2 3.241 1.263 3.509 1.234 -0.269 -1.510
#> 5 ethics_3 2.369 1.121 2.283 0.928 0.086 0.549
#> 6 ethics_4 2.534 1.239 2.566 1.217 -0.032 -0.185
#> 7 work_experi… 17.707 10.540 11.283 11.821 6.424 4.288
#> 8 trust_parli… 3.073 0.797 3.019 0.772 0.054 0.480
#> 9 trust_gover… 2.870 0.847 2.642 0.811 0.229 1.918
#> 10 trust_parti… 2.430 0.724 2.358 0.736 0.072 0.703
#> 11 trust_polit… 2.533 0.707 2.396 0.689 0.136 1.369
#> # ℹ 5 more variables: df <dbl>, p <num:.3!>, d <num:.3!>, Levene_p <dbl>,
#> # var_equal <chr>If passing a group variable with more than two unique levels,
t_test() will produce a warning and default to
the first two unique values. You can manually define the levels by
setting the levels argument:
WoJ %>%
t_test(employment, autonomy_selection, autonomy_emphasis)
#> Warning: employment has more than 2 levels, defaulting to first two (Full-time
#> and Part-time). Consider filtering your data or setting levels with the levels
#> argument
#> # A tibble: 2 × 12
#> Variable `M_Full-time` `SD_Full-time` `M_Part-time` `SD_Part-time` Delta_M
#> * <chr> <num:.3!> <num:.3!> <num:.3!> <num:.3!> <num:.>
#> 1 autonomy_se… 3.903 0.782 3.825 0.633 0.078
#> 2 autonomy_em… 4.118 0.781 4.016 0.759 0.102
#> # ℹ 6 more variables: t <num:.3!>, df <dbl>, p <num:.3!>, d <num:.3!>,
#> # Levene_p <dbl>, var_equal <chr>
WoJ %>%
t_test(employment, autonomy_selection, autonomy_emphasis, levels = c("Full-time", "Freelancer"))
#> # A tibble: 2 × 12
#> Variable `M_Full-time` `SD_Full-time` M_Freelancer SD_Freelancer Delta_M t
#> * <chr> <num:.3!> <num:.3!> <num:.3!> <num:.3!> <num:.> <num>
#> 1 autonom… 3.903 0.782 3.765 0.993 0.139 1.724
#> 2 autonom… 4.118 0.781 3.901 0.852 0.217 3.287
#> # ℹ 5 more variables: df <dbl>, p <num:.3!>, d <num:.3!>, Levene_p <dbl>,
#> # var_equal <chr>Additional options include:
-
pooled_sd: By default, the pooled variance will be used the compute Cohen’s \(d\) effect size estimates (\(s = \sqrt\frac{(n_1 - 1)s^2_1 + (n_2 - 1)s^2_2}{n_1 + n_2 - 2}\)). Setpooled_sd = FALSEto use the simple variance estimation instead (\(s = \sqrt\frac{(s^2_1 + s^2_2)}{2}\)). -
paired: Setpaired = TRUEto compute a paired t-Test instead. It is advisable to specify the case-identifying variable withcase_varwhen computing paired t-Tests, as this will make sure that data are properly sorted.
Previously, the (now deprecated) option of var.equal was
also available. This has been overthrown, however, as
t_test() now by default tests for equal variance (using a
Levene test) to decide whether to use pooled variance or to use the
Welch approximation to the degrees of freedom.
t_test() also provides a one-sample t-Test if you
provide a mu argument:
WoJ %>%
t_test(autonomy_emphasis, mu = 3.9)
#> # A tibble: 1 × 9
#> Variable M SD CI_95_LL CI_95_UL Mu t df p
#> * <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
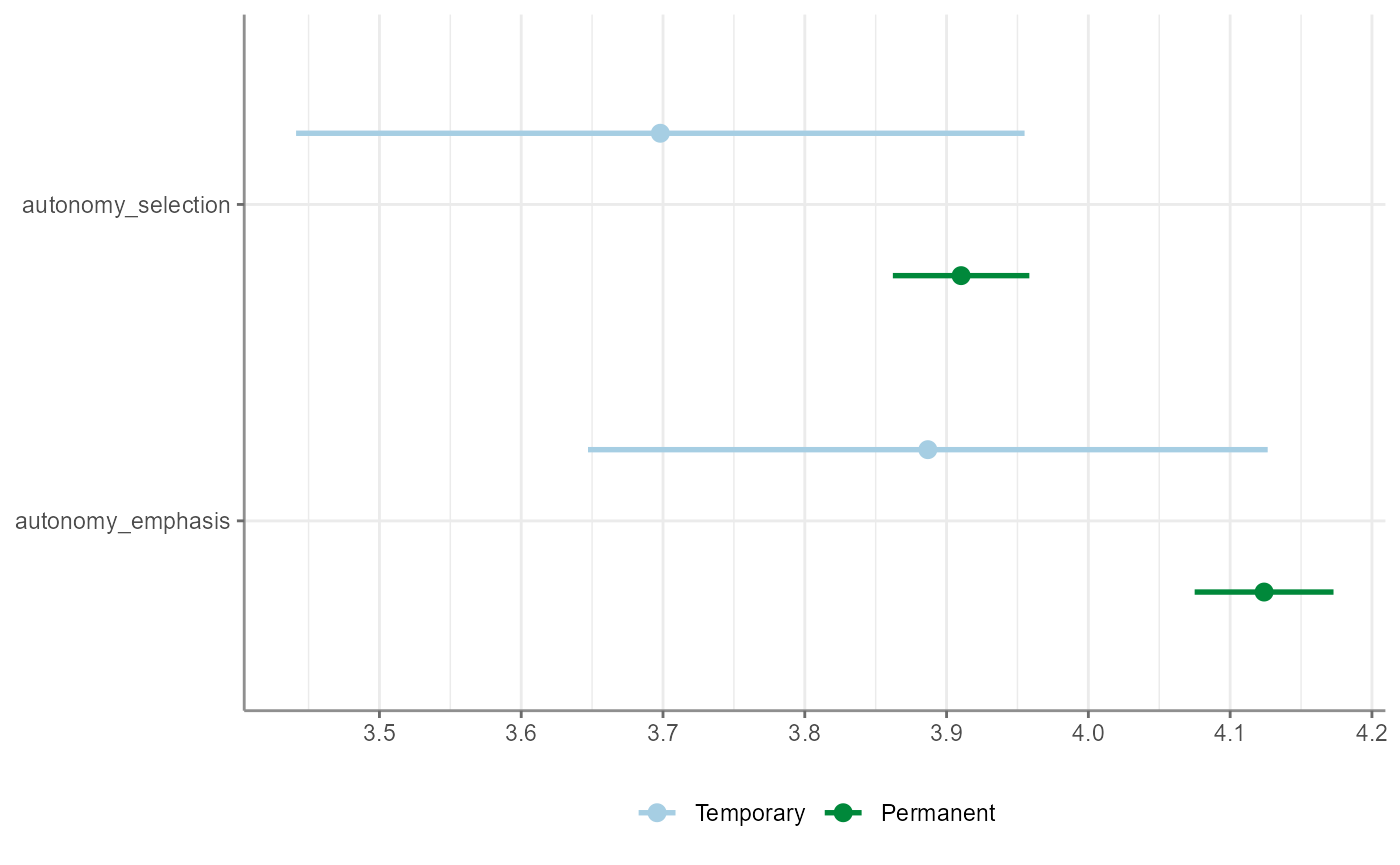
#> 1 autonomy_emphasis 4.08 0.793 4.03 4.12 3.9 7.68 1194 3.23e-14Of course, also the result from t-Tests can be visualized easily as such:
Compute one-way ANOVAs
unianova() will compute one-way ANOVAs for one group
variable and one or more test variables. Output includes test
statistics, \(\eta^2\) effect size
estimates, and \(\omega^2\), if Welch’s
approximation is used to account for unequal variances.
WoJ %>%
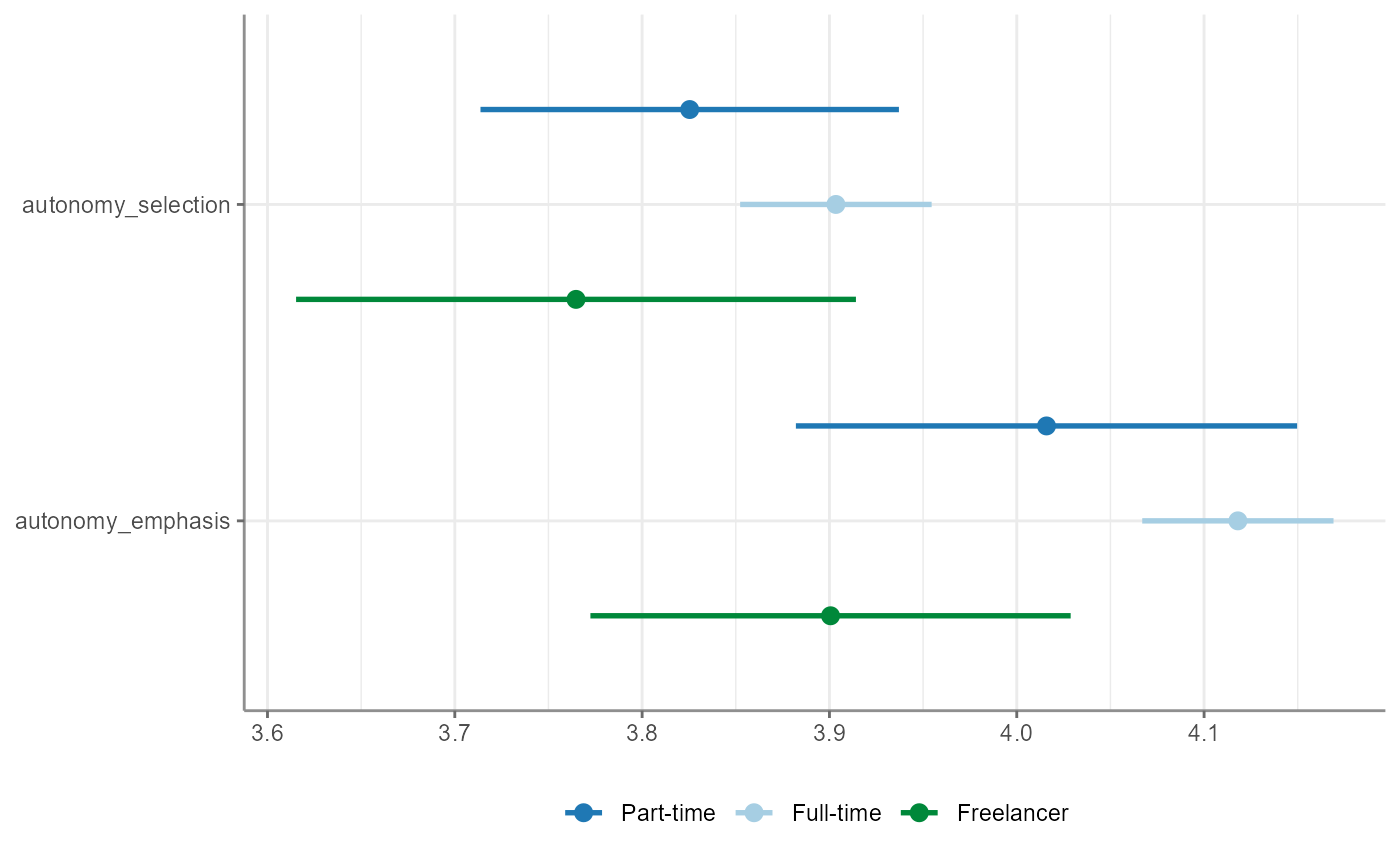
unianova(employment, autonomy_selection, autonomy_emphasis)
#> # A tibble: 2 × 9
#> Variable F df_num df_denom p omega_squared eta_squared Levene_p
#> * <chr> <num> <dbl> <dbl> <num> <num:.3!> <num:.3!> <dbl>
#> 1 autonomy_selec… 2.012 2 251 0.136 0.002 NA 0
#> 2 autonomy_empha… 5.861 2 1192 0.003 NA 0.010 0.175
#> # ℹ 1 more variable: var_equal <chr>Descriptives can be added by setting
descriptives = TRUE. If no test variables are passed, all
numerical variables in the data will be used:
WoJ %>%
unianova(employment, descriptives = TRUE)
#> # A tibble: 11 × 15
#> Variable F df_num df_denom p omega_squared `M_Full-time`
#> * <chr> <num:.3> <dbl> <dbl> <num> <num:.3!> <dbl>
#> 1 autonomy_selection 2.012 2 251 0.136 0.002 3.90
#> 2 autonomy_emphasis 5.861 2 1192 0.003 NA 4.12
#> 3 ethics_1 2.171 2 1197 0.115 NA 1.62
#> 4 ethics_2 2.204 2 1197 0.111 NA 3.24
#> 5 ethics_3 5.823 2 253 0.003 0.007 2.39
#> 6 ethics_4 3.453 2 1197 0.032 NA 2.58
#> 7 work_experience 3.739 2 240 0.025 0.006 17.5
#> 8 trust_parliament 1.527 2 1197 0.218 NA 3.06
#> 9 trust_government 12.864 2 1197 0.000 NA 2.82
#> 10 trust_parties 0.842 2 1197 0.431 NA 2.42
#> 11 trust_politicians 0.328 2 1197 0.721 NA 2.52
#> # ℹ 8 more variables: `SD_Full-time` <dbl>, `M_Part-time` <dbl>,
#> # `SD_Part-time` <dbl>, M_Freelancer <dbl>, SD_Freelancer <dbl>,
#> # eta_squared <num:.3!>, Levene_p <dbl>, var_equal <chr>You can also compute Tukey’s HSD post-hoc tests by setting
post_hoc = TRUE. Results will be added as a
tibble in a list column post_hoc.
WoJ %>%
unianova(employment, autonomy_selection, autonomy_emphasis, post_hoc = TRUE)
#> # A tibble: 2 × 10
#> Variable F df_num df_denom p omega_squared post_hoc eta_squared
#> * <chr> <num> <dbl> <dbl> <num> <num:.3!> <list> <num:.3!>
#> 1 autonomy_selec… 2.012 2 251 0.136 0.002 <df> NA
#> 2 autonomy_empha… 5.861 2 1192 0.003 NA <df> 0.010
#> # ℹ 2 more variables: Levene_p <dbl>, var_equal <chr>These can then be unnested with tidyr::unnest():
WoJ %>%
unianova(employment, autonomy_selection, autonomy_emphasis, post_hoc = TRUE) %>%
dplyr::select(Variable, post_hoc) %>%
tidyr::unnest(post_hoc)
#> # A tibble: 6 × 11
#> Variable Group_Var contrast Delta_M conf_lower conf_upper p d
#> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 autonomy_sel… employme… Full-ti… -0.0780 -0.225 0.0688 0.422 -0.110
#> 2 autonomy_sel… employme… Full-ti… -0.139 -0.329 0.0512 0.199 -0.155
#> 3 autonomy_sel… employme… Part-ti… -0.0607 -0.284 0.163 0.798 -0.0729
#> 4 autonomy_emp… employme… Full-ti… -0.102 -0.278 0.0741 0.362 -0.133
#> 5 autonomy_emp… employme… Full-ti… -0.217 -0.372 -0.0629 0.00284 -0.266
#> 6 autonomy_emp… employme… Part-ti… -0.115 -0.333 0.102 0.428 -0.143
#> # ℹ 3 more variables: se <dbl>, t <dbl>, df <dbl>Visualize one-way ANOVAs the way you visualize almost everything in
tidycomm:
Compute correlation tables and matrices
correlate() will compute correlations for all
combinations of the passed variables:
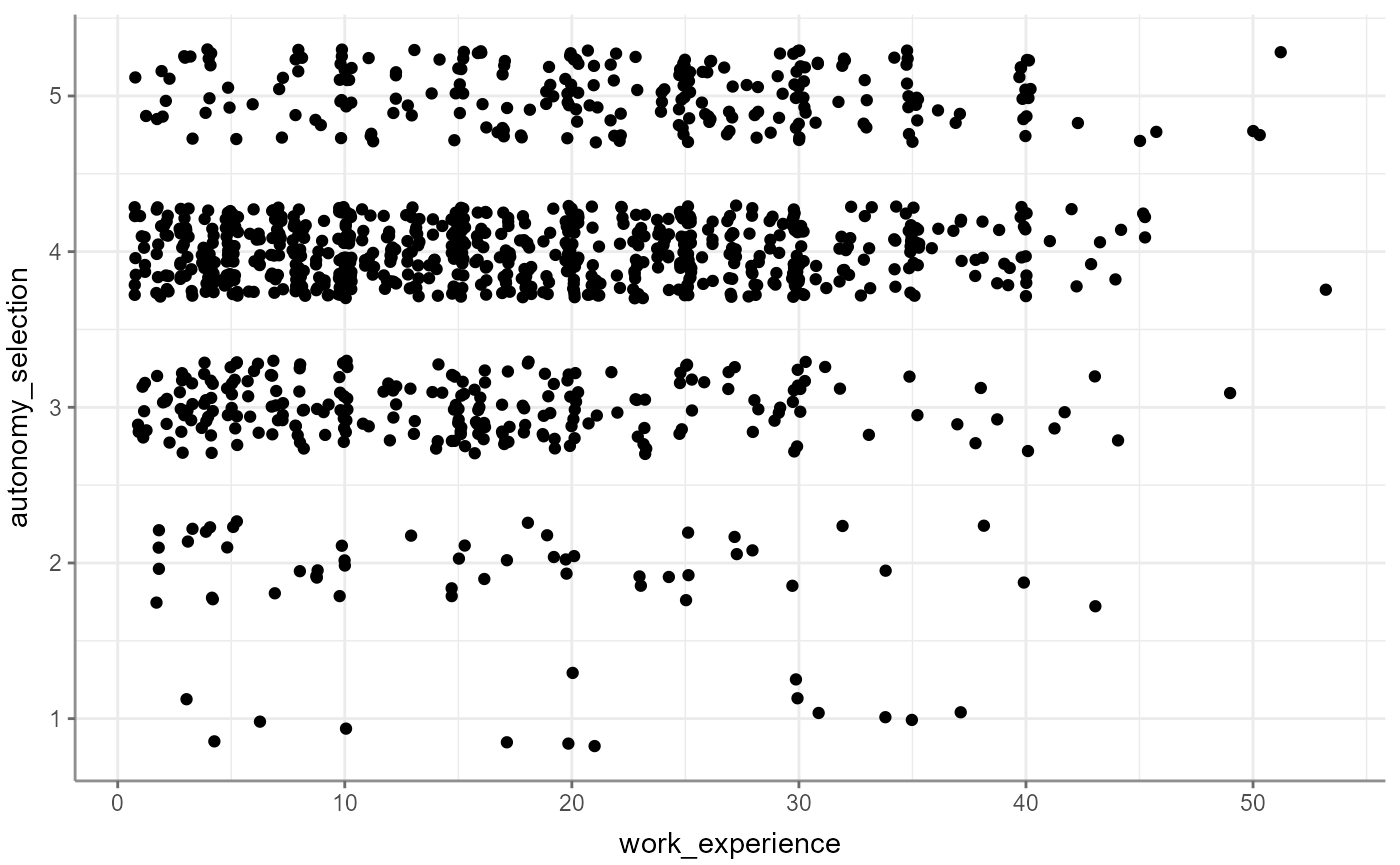
WoJ %>%
correlate(work_experience, autonomy_selection, autonomy_emphasis)
#> # A tibble: 3 × 6
#> x y r df p n
#> * <chr> <chr> <dbl> <int> <dbl> <int>
#> 1 work_experience autonomy_selection 0.161 1182 2.71e- 8 1184
#> 2 work_experience autonomy_emphasis 0.155 1180 8.87e- 8 1182
#> 3 autonomy_selection autonomy_emphasis 0.644 1192 4.83e-141 1194If no variables passed, correlations for all combinations of numerical variables will be computed:
WoJ %>%
correlate()
#> # A tibble: 55 × 6
#> x y r df p n
#> * <chr> <chr> <dbl> <int> <dbl> <int>
#> 1 autonomy_selection autonomy_emphasis 0.644 1192 4.83e-141 1194
#> 2 autonomy_selection ethics_1 -0.0766 1195 7.98e- 3 1197
#> 3 autonomy_selection ethics_2 -0.0274 1195 3.43e- 1 1197
#> 4 autonomy_selection ethics_3 -0.0257 1195 3.73e- 1 1197
#> 5 autonomy_selection ethics_4 -0.0781 1195 6.89e- 3 1197
#> 6 autonomy_selection work_experience 0.161 1182 2.71e- 8 1184
#> 7 autonomy_selection trust_parliament -0.00840 1195 7.72e- 1 1197
#> 8 autonomy_selection trust_government 0.0414 1195 1.53e- 1 1197
#> 9 autonomy_selection trust_parties 0.0269 1195 3.52e- 1 1197
#> 10 autonomy_selection trust_politicians 0.0109 1195 7.07e- 1 1197
#> # ℹ 45 more rowsSpecify a focus variable using the with parameter to
correlate all other variables with this focus variable.
WoJ %>%
correlate(autonomy_selection, autonomy_emphasis, with = work_experience)
#> # A tibble: 2 × 6
#> x y r df p n
#> * <chr> <chr> <dbl> <int> <dbl> <int>
#> 1 work_experience autonomy_selection 0.161 1182 0.0000000271 1184
#> 2 work_experience autonomy_emphasis 0.155 1180 0.0000000887 1182Run a partial correlation by designating three variables along with
the partial parameter.
WoJ %>%
correlate(autonomy_selection, autonomy_emphasis, partial = work_experience)
#> # A tibble: 1 × 7
#> x y z r df p n
#> * <chr> <chr> <chr> <dbl> <dbl> <dbl> <int>
#> 1 autonomy_selection autonomy_emphasis work_experie… 0.637 1178 3.07e-135 1181Visualize correlations by passing the results on to the
visualize() function:
If you provide more than two variables, you automatically get a correlogram (the same you would get if you convert correlations to a correlation matrix):
WoJ %>%
correlate(work_experience, autonomy_selection, autonomy_emphasis) %>%
visualize()
#> Registered S3 method overwritten by 'GGally':
#> method from
#> +.gg ggplot2
By default, Pearson’s product-moment correlations coefficients (\(r\)) will be computed. Set
method to "kendall" to obtain Kendall’s \(\tau\) or to "spearman" to
obtain Spearman’s \(\rho\) instead.
To obtain a correlation matrix, pass the output of
correlate() to to_correlation_matrix():
WoJ %>%
correlate(work_experience, autonomy_selection, autonomy_emphasis) %>%
to_correlation_matrix()
#> # A tibble: 3 × 4
#> r work_experience autonomy_selection autonomy_emphasis
#> * <chr> <dbl> <dbl> <dbl>
#> 1 work_experience 1 0.161 0.155
#> 2 autonomy_selection 0.161 1 0.644
#> 3 autonomy_emphasis 0.155 0.644 1Compute linear regressions
regress() will create a linear regression on one
dependent variable with a flexible number of independent variables.
Independent variables can thereby be continuous, dichotomous, and
factorial (in which case each factor level will be translated into a
dichotomous dummy variable version):
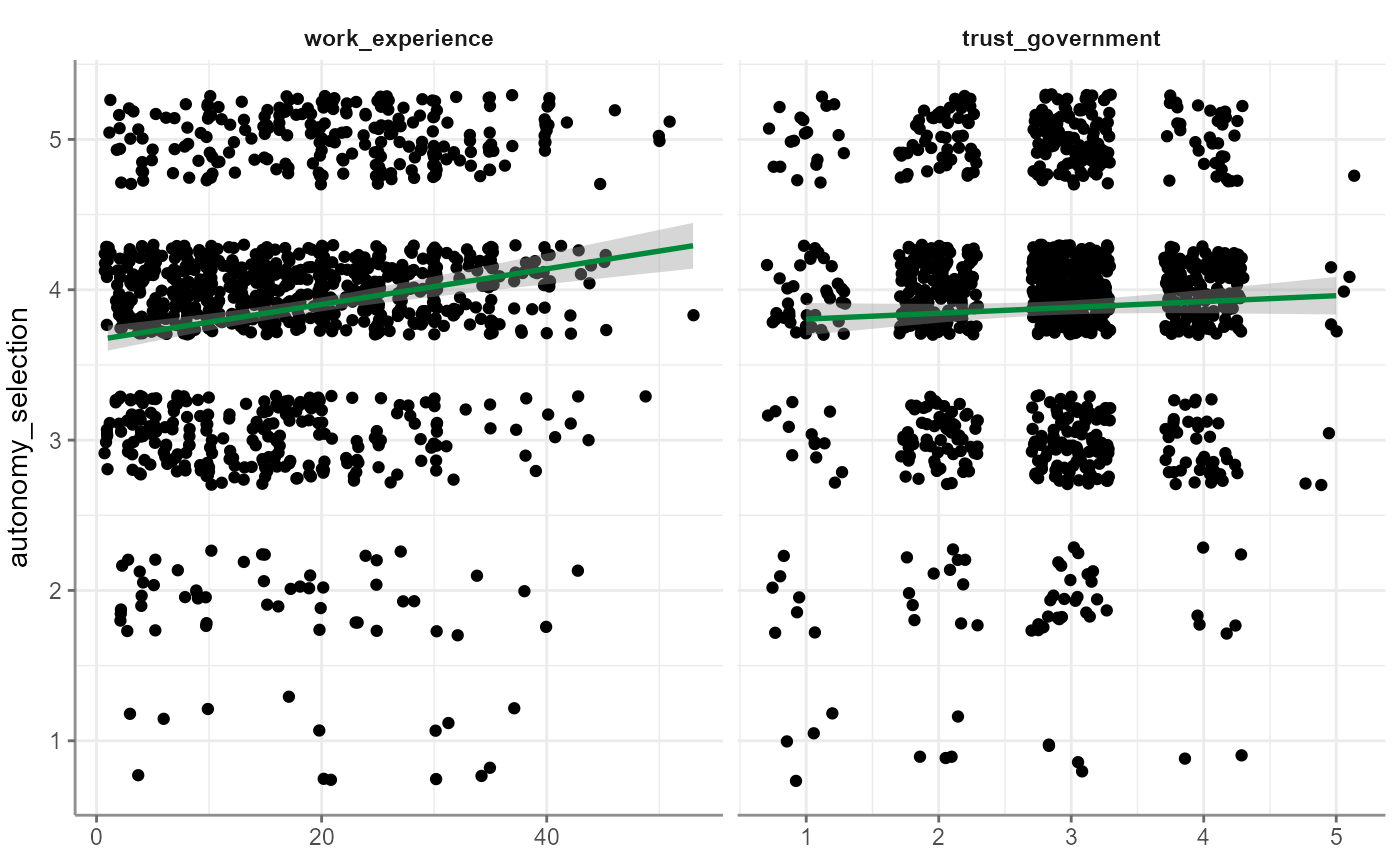
WoJ %>%
regress(autonomy_selection, work_experience, trust_government)
#> # A tibble: 3 × 6
#> Variable B StdErr beta t p
#> * <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 (Intercept) 3.52 0.0906 NA 38.8 3.02e-213
#> 2 work_experience 0.0121 0.00211 0.164 5.72 1.35e- 8
#> 3 trust_government 0.0501 0.0271 0.0531 1.85 6.49e- 2
#> # F(2, 1181) = 17.400584, p = 0.000000, R-square = 0.028624The function automatically adds standardized beta values to the expected linear-regression output. You can also opt in to calculate up to three precondition checks:
WoJ %>%
regress(autonomy_selection, work_experience, trust_government,
check_independenterrors = TRUE,
check_multicollinearity = TRUE,
check_homoscedasticity = TRUE)
#> # A tibble: 3 × 8
#> Variable B StdErr beta t p VIF tolerance
#> * <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 (Intercept) 3.52 0.0906 NA 38.8 3.02e-213 NA NA
#> 2 work_experience 0.0121 0.00211 0.164 5.72 1.35e- 8 1.01 0.995
#> 3 trust_government 0.0501 0.0271 0.0531 1.85 6.49e- 2 1.01 0.995
#> # F(2, 1181) = 17.400584, p = 0.000000, R-square = 0.028624
#> - Check for independent errors: Durbin-Watson = 1.928431 (p = 0.220000)
#> - Check for homoscedasticity: Breusch-Pagan = 0.181605 (p = 0.669997)
#> - Check for multicollinearity: VIF/tolerance added to outputFor linear regressions, a number of visualizations are possible. The default one is the visualization of the result(s), is that the dependent variable is correlated with each of the independent variables separately and a linear model is presented in these:
Alternatively you can visualize precondition-check-assisting depictions. Correlograms among independent variables, for example:
WoJ %>%
regress(autonomy_selection, work_experience, trust_government) %>%
visualize(which = "correlogram")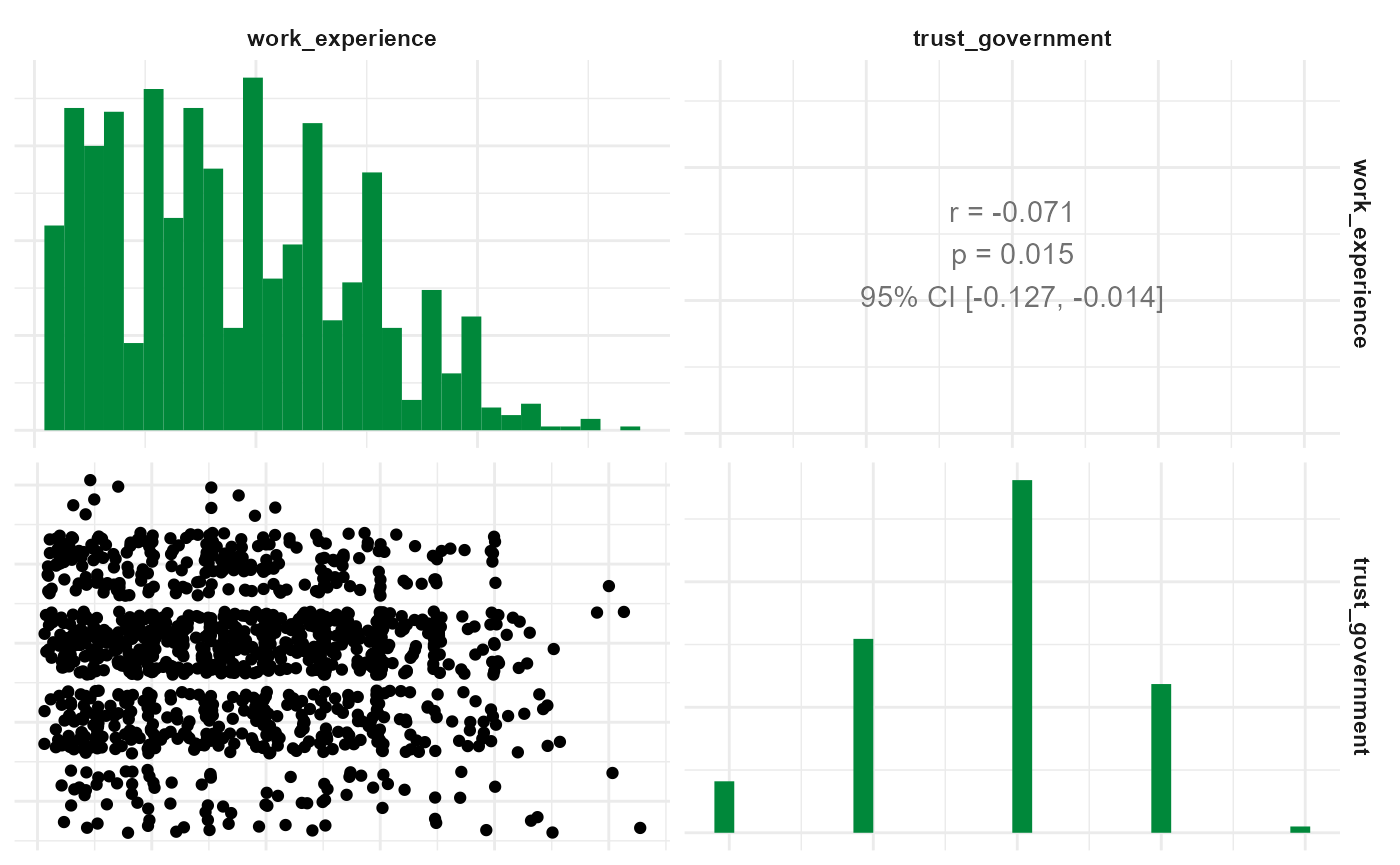
Next up, visualize a residuals-versus-fitted plot to determine distributions:
WoJ %>%
regress(autonomy_selection, work_experience, trust_government) %>%
visualize(which = "resfit")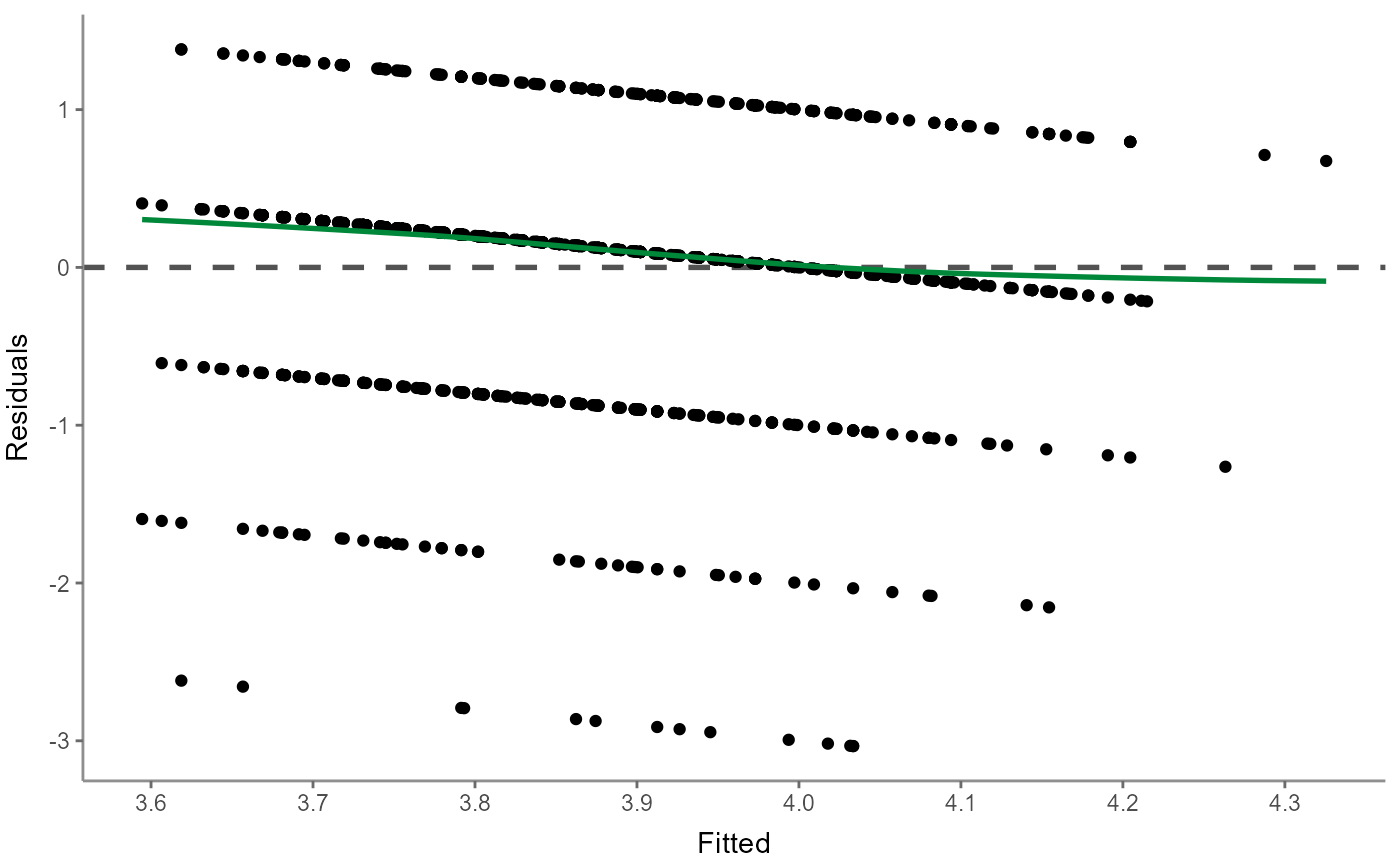
Or use a (normal) probability-probability plot to check for multicollinearity:
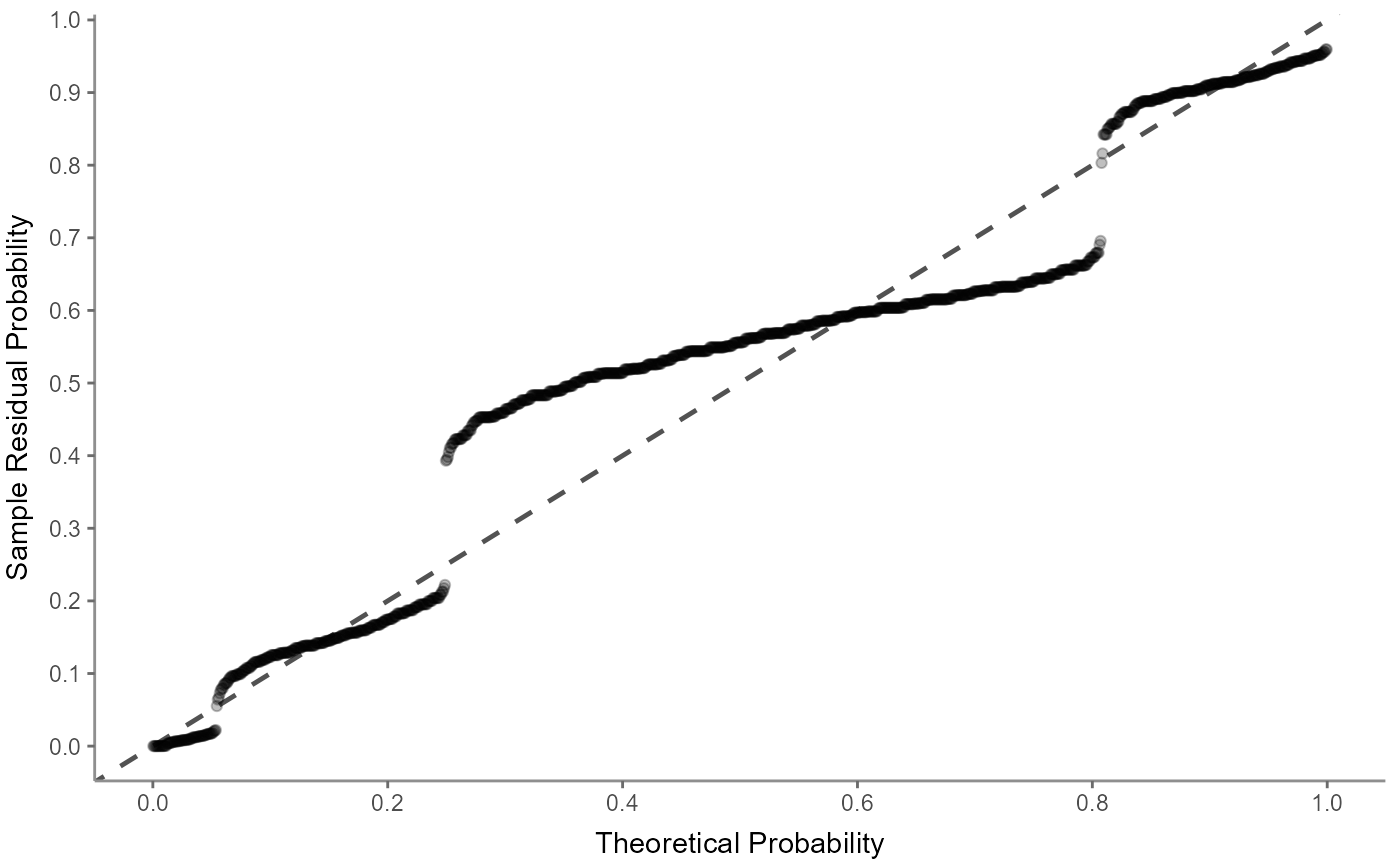
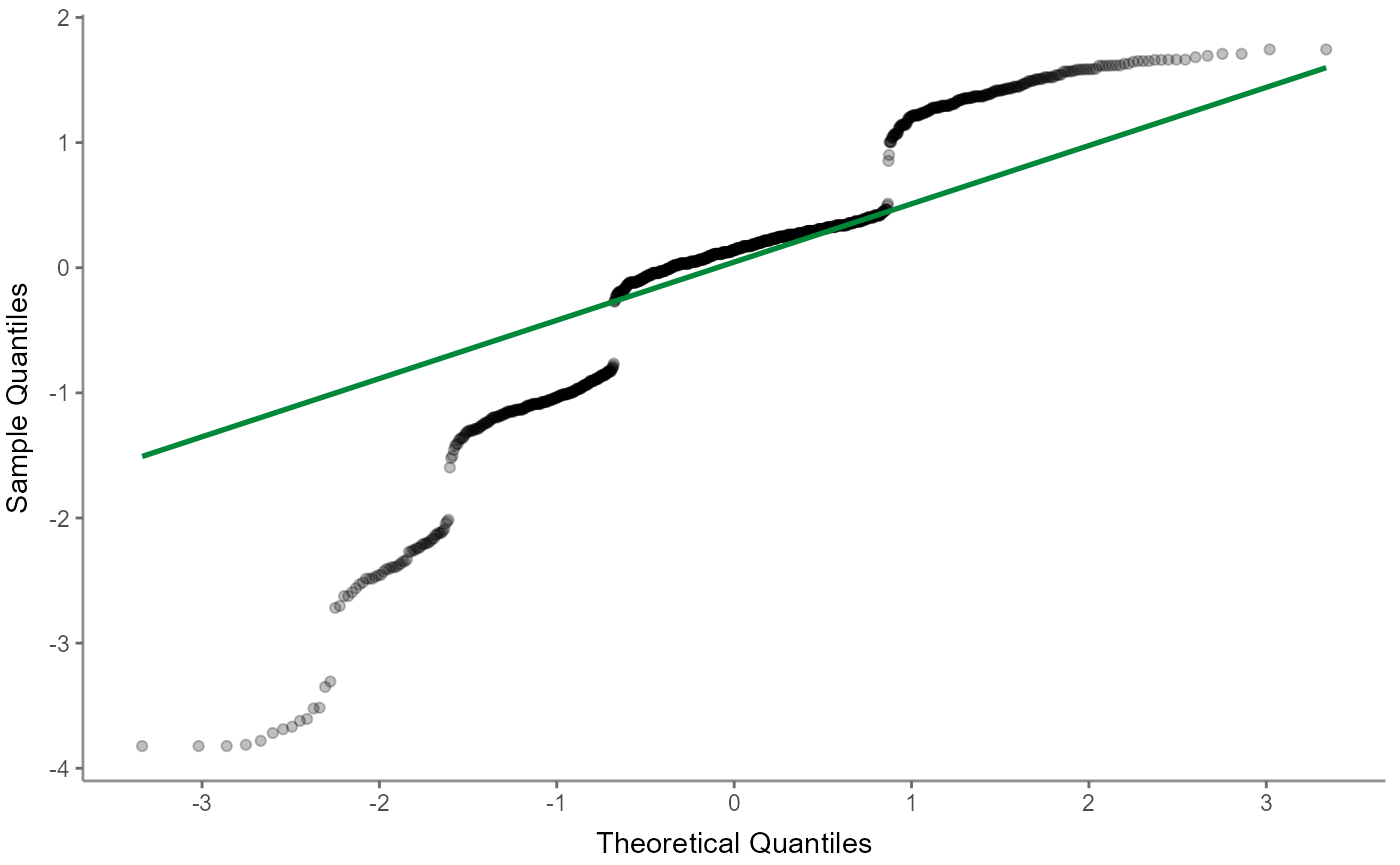
The (normal) quantile-quantile plot also helps checking for multicollinearity but focuses more on outliers:
Next up, the scale-location (sometimes also called spread-location) plot checks whether residuals are spread equally to help check for homoscedasticity:
WoJ %>%
regress(autonomy_selection, work_experience, trust_government) %>%
visualize(which = "scaloc")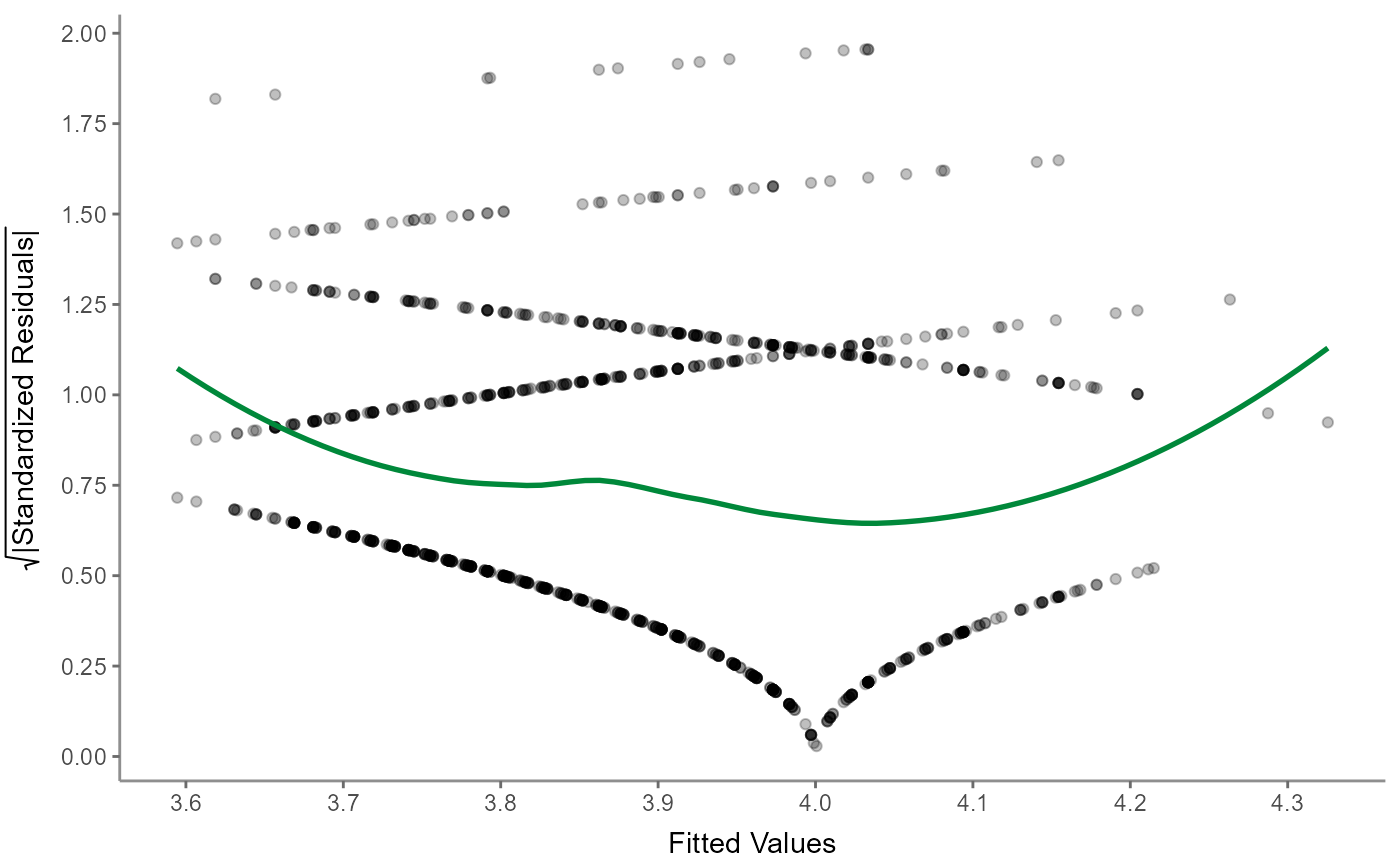
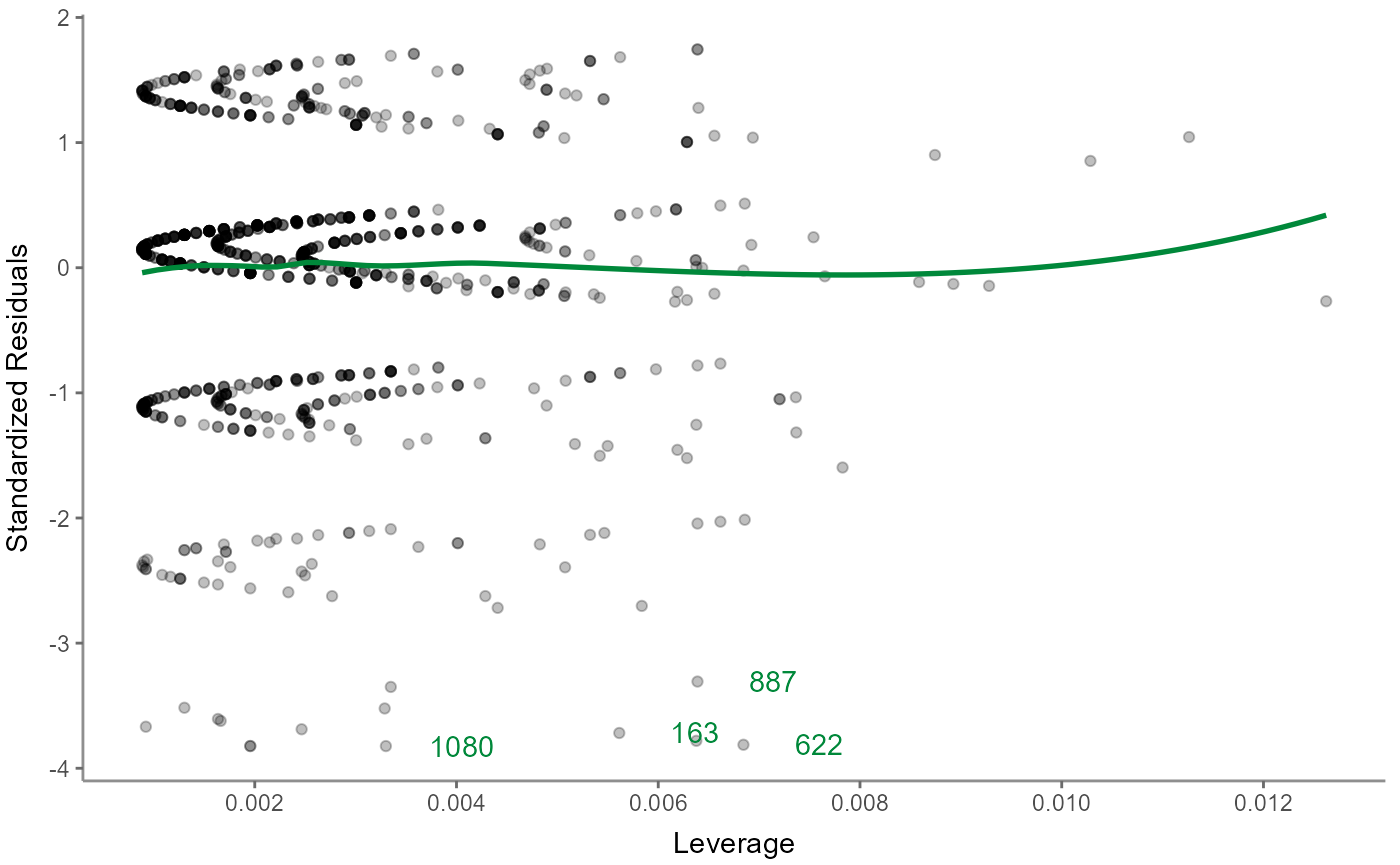
Finally, visualize the residuals-versus-leverage plot to check for influential outliers affecting the final model more than the rest of the data:
WoJ %>%
regress(autonomy_selection, work_experience, trust_government) %>%
visualize(which = "reslev")